How to create an algorithm? This guide dives deep into the world of algorithmic design, from fundamental concepts to practical implementation. We’ll explore various types of algorithms, examine effective design strategies, and learn how to translate your ideas into working code. Understanding algorithms is key to solving complex problems efficiently and effectively.
This comprehensive guide will walk you through the entire process, providing detailed explanations, practical examples, and actionable insights. Learn how to break down complex problems, choose the right algorithm, and implement it with precision. You’ll discover how to optimize your code for speed and efficiency.
Fundamental Concepts of Algorithms

Algorithms are the fundamental building blocks of computer science, providing step-by-step procedures for solving problems. They are crucial for everything from simple calculations to complex data analysis. Understanding different types of algorithms and their characteristics is essential for designing efficient and effective solutions. This section explores the core concepts of algorithms, highlighting their various forms and practical applications.A well-designed algorithm not only solves a problem but does so in a manner that is both accurate and optimized for time and resource consumption.
Creating a robust algorithm involves meticulous planning and careful consideration of the steps involved. For example, when troubleshooting feeding issues like clicking noises during bottle feeding, a logical approach, similar to algorithm design, can help. This process requires identifying the potential causes, testing different solutions, and refining the approach until the issue is resolved, which mirrors the iterative nature of algorithm development.
Further resources for resolving bottle-feeding problems can be found here: how to fix clicking while bottle feeding. Ultimately, both algorithmic design and problem-solving demand a systematic and organized methodology.
Understanding the different approaches to algorithm design allows for choosing the most appropriate method for a given task.
Types of Algorithms
Algorithms are categorized based on their approaches to problem-solving. Understanding these categories is crucial for selecting the most suitable algorithm for a particular task.
- Iterative Algorithms: These algorithms employ loops or repetitions to achieve a solution. They repeatedly execute a set of instructions until a specific condition is met. A common example is calculating the factorial of a number using repeated multiplications.
- Recursive Algorithms: These algorithms solve a problem by breaking it down into smaller, self-similar subproblems. They call themselves within their own definition until a base case is reached. A classic example is calculating Fibonacci numbers, where each number is the sum of the two preceding ones.
- Greedy Algorithms: These algorithms make locally optimal choices at each step, hoping to arrive at a globally optimal solution. A common application is finding the shortest path in a graph, where the algorithm always selects the edge with the smallest weight.
- Divide-and-Conquer Algorithms: These algorithms divide a problem into smaller subproblems, solve them recursively, and then combine the solutions to obtain the final solution. An efficient example is the merge sort algorithm for sorting a list of items.
Examples in Everyday Life
Algorithms are not just theoretical concepts; they are embedded in countless everyday activities.
Crafting a robust algorithm involves meticulous planning and a step-by-step approach, mirroring the process of creating a Linux partition. Understanding the intricacies of disk management, like those found in linux how to create partition , highlights the importance of precise instructions and logical sequencing. Ultimately, both tasks demand careful consideration of every detail to achieve the desired outcome.
- Sorting a list of items: Ordering items alphabetically in a dictionary or numerically in a phone book are examples of sorting algorithms. Different sorting algorithms have varying efficiency, impacting the speed of the process.
- Finding the shortest path: Planning a route using a navigation app or determining the most efficient delivery route for packages are examples of finding the shortest path algorithms.
- Searching for information: Searching for a specific item in a large database or using a search engine to find relevant information online relies on search algorithms. Efficient search algorithms are crucial for fast results in large datasets.
Efficiency and Time Complexity
Algorithm efficiency is a critical factor in its effectiveness. An efficient algorithm minimizes the resources (time and memory) needed to solve a problem. Time complexity, a measure of the algorithm’s running time as the input size grows, is a key metric for evaluating efficiency.
- Importance of Efficiency: In many applications, the speed of an algorithm can be the difference between a usable and unusable system. Faster algorithms lead to faster response times and greater scalability.
- Time Complexity Analysis: Time complexity is analyzed by considering the number of operations an algorithm performs as a function of the input size. This analysis helps predict the algorithm’s performance for different input sizes.
Comparison of Sorting Algorithms
The table below illustrates the time complexities of different sorting algorithms, highlighting their performance characteristics.
| Sorting Algorithm | Best Case Time Complexity | Average Case Time Complexity | Worst Case Time Complexity |
|---|---|---|---|
| Bubble Sort | O(n) | O(n2) | O(n2) |
| Insertion Sort | O(n) | O(n2) | O(n2) |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) |
Time complexity is expressed using Big O notation, which describes the upper bound of the algorithm’s growth rate.
Crafting a robust algorithm involves meticulous planning and a step-by-step approach, mirroring the process of creating a Linux partition. Understanding the intricacies of disk management, like those found in linux how to create partition , highlights the importance of precise instructions and logical sequencing. Ultimately, both tasks demand careful consideration of every detail to achieve the desired outcome.
Algorithm Design Techniques
Algorithm design techniques are crucial for translating complex problems into efficient and elegant solutions. Mastering these strategies empowers developers to tackle intricate scenarios, leading to optimized code and improved performance. These methods allow for the breakdown of problems into smaller, more manageable parts, which are then combined to form the overall solution.Effective algorithm design is not just about finding a solution, but about finding thebest* solution.
This often involves careful consideration of the trade-offs between different approaches, balancing factors like time complexity, space complexity, and the overall clarity of the code. Understanding the nuances of various design strategies is key to achieving this balance.
Dynamic Programming
Dynamic programming is a powerful technique for solving optimization problems by breaking them down into smaller overlapping subproblems. This approach stores the solutions to these subproblems, avoiding redundant calculations. By memoizing solutions, dynamic programming significantly improves efficiency, especially for problems exhibiting overlapping subproblems.
- Overlapping Subproblems: A problem exhibits overlapping subproblems if the same subproblems are solved repeatedly during the solution process. Dynamic programming excels at tackling such situations, as it avoids redundant calculations by storing the solutions to these subproblems.
- Optimal Substructure: The problem should have an optimal substructure, meaning that an optimal solution to the whole problem can be constructed from optimal solutions to its subproblems. This property is fundamental to the validity of dynamic programming solutions.
Example: Finding the shortest path in a graph. This problem has overlapping subproblems as the shortest paths to intermediate nodes are calculated multiple times. The optimal substructure lies in the fact that the shortest path from a starting node to any other node can be constructed from the shortest paths to intermediate nodes.
Backtracking
Backtracking is a general algorithmic technique for finding all (or some) solutions to problems that can be expressed as a sequence of choices. It involves exploring potential solutions step-by-step, and if a choice leads to a dead end, the algorithm backtracks to reconsider previous choices. Backtracking is particularly effective for problems involving combinatorial searches.
- Systematic Search: Backtracking systematically explores possible solutions by making choices and then undoing them if they don’t lead to a viable solution. This methodical approach guarantees that all possible solutions are considered.
- Constraint Satisfaction: Many problems involve constraints on the choices that can be made. Backtracking effectively handles such constraints by discarding branches that violate these constraints.
Example: The Eight Queens problem, where the goal is to place eight queens on a chessboard such that no two queens threaten each other. Backtracking systematically explores possible placements of queens, backing up when a conflict is detected.
Crafting a robust algorithm involves meticulous planning and a step-by-step approach, mirroring the process of creating a Linux partition. Understanding the intricacies of disk management, like those found in linux how to create partition , highlights the importance of precise instructions and logical sequencing. Ultimately, both tasks demand careful consideration of every detail to achieve the desired outcome.
Divide and Conquer
Divide and conquer is a powerful approach that breaks down a problem into smaller subproblems, solves them recursively, and then combines the results to solve the original problem. This technique often leads to efficient solutions, particularly for problems with a recursive structure.
- Decomposition: The core idea is to decompose a problem into smaller, more manageable subproblems that are easier to solve.
- Conquest: These subproblems are solved recursively. The efficiency often depends on the efficiency of the subproblem solutions.
- Combination: The solutions to the subproblems are combined to produce the solution to the original problem.
Example: Merge sort. This algorithm recursively divides a list into smaller sublists, sorts them, and then merges them back together. This recursive strategy leads to an efficient sorting algorithm.
Pseudocode, How to create an algorithm
Pseudocode is a high-level description of an algorithm, using a combination of natural language and programming-like constructs. It serves as a bridge between the problem definition and the actual code implementation, helping to clarify the algorithm’s logic and structure before writing actual code.
- Clarity and Readability: Pseudocode emphasizes the logic of the algorithm, making it easier to understand and communicate to others.
- Abstraction: Pseudocode avoids the intricacies of specific programming languages, allowing for a focus on the core algorithmic steps.
- Implementation Guidance: It serves as a blueprint for translating the algorithm into a concrete programming language.
Example: Pseudocode for a function to find the largest element in an array:
function findLargest(array): largest = array[0] for each element in array: if element > largest: largest = element return largest
Comparison of Algorithm Design Techniques
| Technique | Advantages | Disadvantages |
|---|---|---|
| Dynamic Programming | High efficiency for overlapping subproblems, optimal solutions | Can be complex to design, requires careful analysis of subproblems |
| Backtracking | Systematic search, finds all solutions | Can be inefficient for large search spaces, might not find an optimal solution |
| Divide and Conquer | Efficient for problems with recursive structure, often leads to optimal solutions | Can be complex to implement, might not be suitable for all problems |
Implementing Algorithms
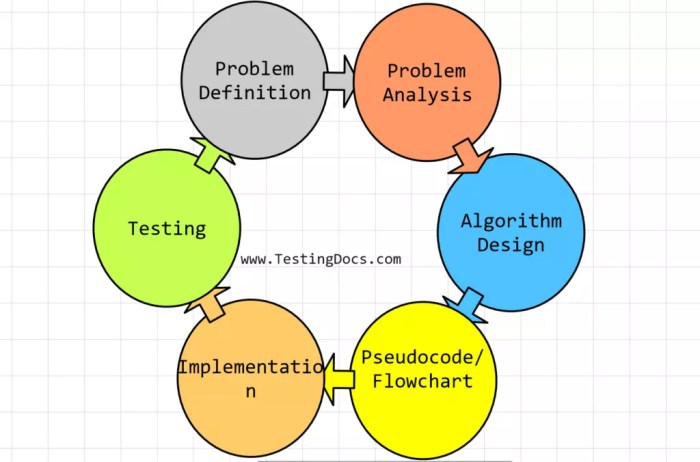
Bringing an algorithm to life requires translating its pseudocode into a specific programming language. This crucial step bridges the gap between theoretical design and practical application. Effective implementation depends on a deep understanding of the chosen language’s syntax and the nuances of the algorithm itself. Careful attention to detail is paramount, ensuring the code accurately reflects the intended logic and functions as anticipated.
Translating Pseudocode to Code
Translating an algorithm from pseudocode to a concrete programming language involves several key steps. First, identify the core logic and operations defined in the pseudocode. Then, map these steps to the corresponding constructs in the target language (e.g., loops, conditional statements, functions). This process necessitates a thorough understanding of the programming language’s syntax and semantics. Carefully consider variable types and data structures.
Importance of Data Structures
Data structures are fundamental to efficient algorithm implementation. They dictate how data is organized and accessed, directly influencing the algorithm’s speed and memory usage. Choosing the appropriate data structure for a particular algorithm can significantly impact performance, potentially improving speed by orders of magnitude. The selection depends on the specific operations required and the characteristics of the data.
Using Data Structures for Optimal Performance
Different data structures excel at different tasks. Arrays provide fast random access, ideal for scenarios needing quick retrieval of elements by index. Linked lists excel at insertion and deletion, making them suitable for dynamic collections where changes are frequent. Trees, like binary search trees, enable efficient searching and sorting operations. Selecting the appropriate structure significantly impacts performance.
Examples of Data Structures and Algorithms
- Arrays: Ideal for storing collections of elements with sequential access. Common algorithms utilizing arrays include sorting algorithms like insertion sort and bubble sort. Arrays are efficient for accessing elements by index, but insertion or deletion can be slow.
- Linked Lists: Excellent for dynamic data structures where insertions and deletions are frequent. Algorithms like insertion and deletion are efficient, but random access is slower than arrays.
- Trees: Essential for hierarchical data and searching. Binary search trees allow for efficient searching, insertion, and deletion operations. Algorithms like tree traversals (inorder, preorder, postorder) are typical.
Table of Common Data Structures and Use Cases
| Data Structure | Description | Use Cases |
|---|---|---|
| Array | Ordered collection of elements | Storing sequences, fast access by index |
| Linked List | Elements connected by pointers | Dynamic insertions/deletions, efficient for frequent changes |
| Binary Search Tree | Nodes with left and right children | Efficient searching, sorting, and range queries |
| Hash Table | Data stored using hash functions | Fast lookups, insertions, and deletions |
Testing and Debugging Algorithms
Thorough testing and debugging are essential for ensuring an algorithm’s correctness and robustness. Unit tests, which isolate individual functions or methods, can verify the correctness of specific parts of the algorithm. Comprehensive test cases should cover various scenarios, including normal cases, boundary conditions, and error handling. Debugging techniques, such as print statements and breakpoints, can help identify the source of errors.
Consider edge cases and potential issues, such as input validation, to avoid unexpected behavior. Testing helps catch errors early in the development process, reducing the likelihood of unexpected results in production.
Final Review
In conclusion, crafting effective algorithms involves a blend of theoretical understanding and practical application. This guide has provided a structured approach to algorithm design, from foundational concepts to real-world implementation. By mastering the techniques presented, you’ll be equipped to tackle complex problems with efficiency and precision. Remember, continuous practice and experimentation are essential for mastering this valuable skill.
Detailed FAQs: How To Create An Algorithm
What are the different types of algorithms?
Algorithms can be categorized in various ways, including iterative, recursive, greedy, and divide-and-conquer algorithms. Each type has its strengths and weaknesses, making the selection crucial for optimal performance.
How do I choose the right algorithm for a problem?
The selection of an algorithm depends on the specific problem’s characteristics, such as the input size, desired output, and constraints. Analyzing time and space complexity is essential for making an informed decision.
What is the role of pseudocode in algorithm design?
Pseudocode acts as a high-level description of an algorithm, allowing for easier understanding and modification before implementation in a specific programming language. It helps visualize the steps and logic without the intricacies of syntax.
How important is testing and debugging in algorithm development?
Rigorous testing and debugging are critical for identifying and resolving errors, ensuring the algorithm functions as intended and produces accurate results. Thorough testing helps prevent unexpected behavior and improves the algorithm’s overall reliability.
